Funciones Trigonométricas
Triángulo rectángulo
Recordamos que un triángulo es rectángulo cuando tiene un ángulo recto, es decir, un ángulo de 90 grados ó radianes.
De los tres lados del triángulo, se llama hipotenusa al lado opuesto al ángulo recto. Los otros dos lados se denominan catetos:
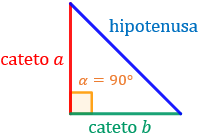
Si conocemos dos lados del triángulo, podemos calcular el otro aplicando el teorema de Pitágoras.
Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno.
Seno y coseno
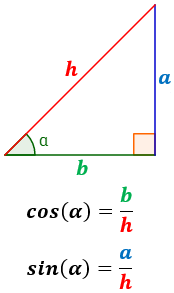
El coseno de un ángulo se define como el cociente del lado contiguo al ángulo y la hipotenusa.
De forma análoga, el seno de se define como el cociente del lado opuesto al ángulo y la hipotenusa.
Nota: si cambiamos de ángulo, cambian los numeradores:
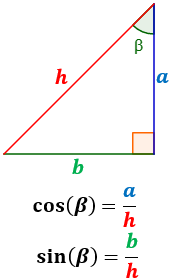
Normalmente, para referirnos al seno de podemos escribir , ó . Y para el coseno, ó .
Nosotros utilizaremos y .
Regla mnemotécnica: el coseno es el lado contiguo entre la hipotenusa y el seno es el lado Opuesto entre la hipotenusa.
Tangente
La tangente del ángulo es el cociente del seno y del coseno de dicho ángulo:
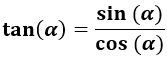
La tangente es el cociente del lado opuesto y del lado contiguo.
La tangente del ángulo puede escribirse como y como , entre otras.
No utilizaremos la tangente en esta página.
Arcoseno y arcocoseno
Si conocemos el seno (o coseno) de un ángulo , podemos conocer el ángulo mediante la función arcoseno (o arcocoseno).
En esta página sólo utilizaremos estas funciones en la calculadora con las teclas (arcoseno) y (arcocoseno).
Nota: hay que tener cuidado con las funciones arcoseno y arcocoseno ya que hay ángulos que tienen el mismo seno o coseno. Por ejemplo, el seno de 45º es el mismo que el de 135º:
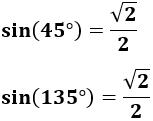
Comentarios
Publicar un comentario